ZKP on Spot Instances: NTT
Giro ResearchJan. 15, 2024
In our previous post, we introduced the idea of using AWS EC2 spot instances for complex ZKP workloads. Specifically, we described in detail a method for computing MSMs. In this article, we will focus on another computationally intensive task: Number Theoretic Transform (NTT).
Why is NTT Useful
Modern ZKP protocols widely use polynomials defined over finite fields as intermediates by encoding data and operations as polynomials and then proving correctness via polynomial commitments that reveal polynomial values at “random” challenge points.
In doing so, we often need to transform existing polynomials into new ones to prove certain properties. Among these transformations, polynomial multiplication are the most cumbersome (divisions can be expressed as multiplications). If we represent two polynomials of order $n$ with their $n+1$ coefficients (i.e., use the coefficient representation), directly computing the coefficients of the product polynomial has time complexity $O(n^2)$ , which is too slow for large $n$. However, if we switch to a different representation where each order-$n$ polynomial is represented by $n+1$ evaluations at some chosen point set (i.e., the point-value representation), multiplications become much easier - all that’s needed is to multiply together the respective evaluations.
Notice, though, that we haven’t yet reduced the complexity of polynomial multiplication, as the resultant polynomial will have order $2n$. Such a polynomial requires $2n+1$ evaluations to represent so we would need to evaluate the original polynomials at more points. Moreover, although polynomial evaluation at arbitrary points is efficient in coefficient form, it is difficult when the polynomial is itself represented as a tuple of evaluations.
This is where NTT comes in. NTT is an algorithm for efficiently evaluating polynomials on a special point set. With a point set of size $n=2^k$, NTT requires only $O(n\log(n))$field operations to evaluate any polynomial of order no larger than $n-1$ at all points. In addition, given the evaluations of some polynomial on this point set, NTT can also efficiently compute the coefficients of this polynomial. In essence, NTT can be used to convert polynomials between coefficient representation and point-value representation so that operations on the polynomial can be done in the more efficient domain.
More specifically, let’s look at how NTT can be used to speed up polynomial multiplication. Given two polynomials of order $n$ in coefficient form, we first convert them to point-value representation by evaluating each polynomial on $2n+1$ points with NTT. We then multiply the evaluations of two polynomials together to get the product polynomial in point-value representation. Finally, we use NTT again to derive the coefficients of the product polynomial. Each NTT takes $O(n\log(n))$time and the multiplication takes $O(n)$ time, so the overall complexity is $O(n\log(n))$. This is much faster than the naive $O(n^2)$ multiplication algorithm.
How NTT Works
Consider a finite field $\mathbb{F}_p$, an integer $n = 2^t$, and the $n\text{-th}$ root of unity $\epsilon_n$ (satisfying $\epsilon_n^n = 1$, and $\epsilon_n^{i} \neq 1$ for $1 \leq i \leq n-1$). Roots of unity have three very useful properties.
- Periodicity: $\epsilon_n^{n+k} = \epsilon_n^{k}$
- Symmetry: $\epsilon_n^{k+n/2} = -\epsilon_n^{k}$
- Scalability: $\epsilon_n^{2k} = \epsilon_{n/2}^{k}$
Given a polynomial $f(x) = \sum_{i=0}^{n-1} a_i x^{i}$ of order $n-1$ on $\mathbb{F}_p$, NTT is an algorithm that efficiently computes $f(\epsilon_n^k)$ for all $k \in {0,1,2,\cdots, n-1}$. Here’s a step-by-step walkthrough.
- Split the coefficients according to their parities.
\begin{equation} f(\epsilon_n^k) = \sum_{i=0}^{n-1}a_i \epsilon_n^{ik} = \sum_{i=0}^{ n/2-1} a_{2i}\epsilon_n^{2ik} + \sum_{i=0}^{n/2-1} a_{2i+1}\epsilon_n^{2ik+k} = \sum_{ i=0}^{n/2-1} a_{2i}\epsilon_n^{2ik} + \epsilon_n^{k}\sum_{i=0}^{n/2-1} a_{2i+1} \epsilon_n^{2ik}. \end{equation}
- Using scalability, we get:
\begin{equation} f(\epsilon_n^k) = \sum_{i=0}^{n/2-1} a_{2i}\epsilon_n^{2ik} + \epsilon_n^{k}\sum_{i=0}^{n /2-1} a_{2i+1}\epsilon_n^{2ik} = \sum_{i=0}^{n/2-1} a_{2i}\epsilon_{n/2}^{ik} + \epsilon_n^{k}\sum_{i=0}^{n/2-1} a_{2i+1}\epsilon_{n/2}^{ik}. \tag{1} \label{1} \end{equation}
- Using periodicity and symmetry, we have:
\begin{equation} f(\epsilon_n^{k+n/2}) = \sum_{i=0}^{n/2-1} a_{2i}\epsilon_{n/2}^{ik} - \epsilon_n^{k }\sum_{i=0}^{n/2-1} a_{2i+1}\epsilon_{n/2}^{ik}. \tag{2} \label{2} \end{equation}
On a high level, NTT takes a divide-and-conquer approach. The original polynomial of order $n-1$ can be divided by parity and transformed into two smaller polynomials of order $n/2 - 1$ using equations \eqref{1} and \eqref{2}. By recursively applying this method, the problem will eventually be reduced into trivial evaluations of constant polynomials in $t$ steps.
Take $n = 8$ as an example. The NTT algorithm is depicted in the diagram, where $x[i]$ corresponds to $a_i$, $X[i]$ corresponds to $ f(\epsilon_n ^i)$, and $W_N^k$ (called twiddle factors) corresponds to $\epsilon_n^{k}$ in equations \eqref{1} and \eqref{2}.
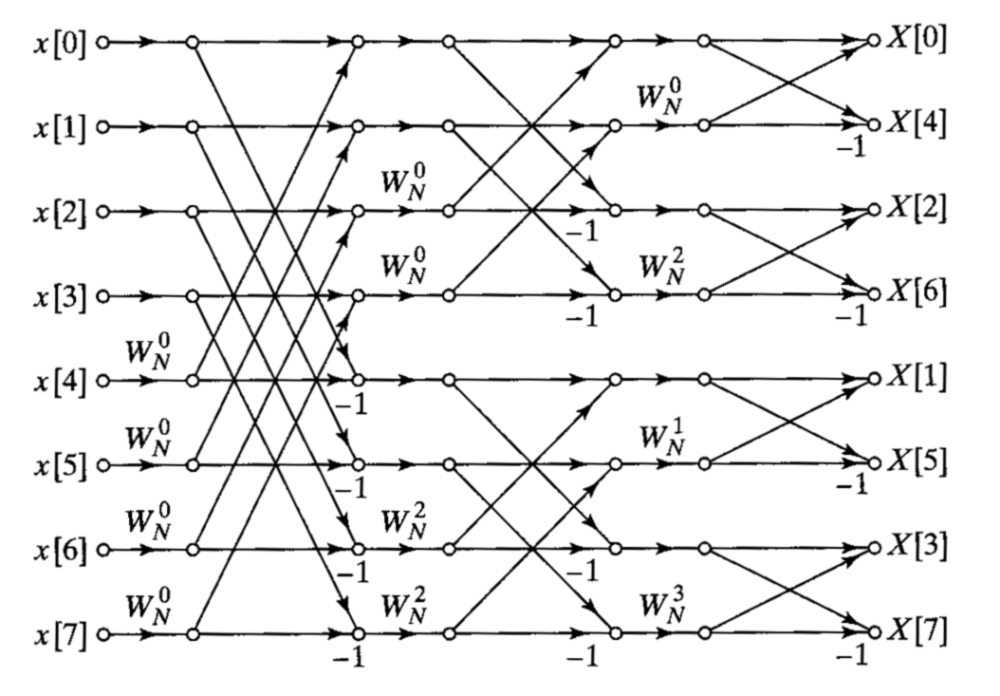
It is easy to obtain from equations \eqref{1} and \eqref{2} that combining two NTT results of size $n/2$ into one NTT result of size $n$ requires $n$ multiplications (muls) and $n$ additions/subtractions (adds) on $\mathbb{F}_p$. More specifically, for a pair $f(\epsilon_n^k)$ and $f(\epsilon_n^{k+n/2})$, let $n/2$-sized NTT results be $a=\sum_{i=0}^{n/2-1} a_{2i}\epsilon_{n/2}^{ik}$ and $b=\sum_{i=0}^{n/2-1} a_{2i+1}\epsilon_{n/2}^{ik}$. We first multiply $b$ with twiddle factor $\epsilon_n^{k}$ to derive $c=b\cdot \epsilon_n^{k }$, and then we get $f(\epsilon_n^k) = a + c$ and $f(\epsilon_n^{k+n/2}) = a - c$.
The time complexity of NTT algorithm with size $n = 2^t$ is $t\cdot n$ muls plus $t \cdot n$ adds on $\mathbb{F}_p$. And the space complexity of NTT with size $n$ is $O(n)$.
NTT on Spot Instances
Recall that AWS EC2 spot instances allow users to make significant savings on cloud computing cost. The tradeoff is that those instances may be terminated at any arbitrary time with very short advance notice (2 minutes). When using spot instances to compute large size NTTs for ZKP generation, these interruptions are the main challenge we need to tackle.
In the diagram above, NTT computation proceeds layer by layer from left to right. Values in layer 1 is the initial inputs (reordered coefficients of the polynomial), and values of layer 2 are computed using values of layer 1, and so on. When computing the values of the $i+1$th layer, only values of layer $i$ are used, so we can use values in any single layer (along with the layer index) to derive the final answer.
Upon receiving the interruption notice, we can simply store the latest computed layer to disk, which can be read back at a later time to resume computation. The overhead for persisting those intermediate values is proportional to the NTT size $n$, there is almost no computing overhead.